Micro-resonator frequency combs (“Microcombs”)
The development of optical frequency combs1, and notably self-referencing2, has revolutionized precision measurements over the past decade, and enabled counting of the cycles of light. Frequency combs, for which Hall and Haensch shared the Physics Nobel Prize in 2005 has enabled dramatic advances in timekeeping, metrology and spectroscopy. In 2007, research on microresonators resulted in the discovery of a novel method5,38 to generate optical frequency combs using parametric frequency conversion in optical microresonators3,4. This unexpected observation broke with the conventional dogma that optical combs can only be generated with mode locked pulsed laser sources. Instead this work showed that a CW laser can be converted into a broadband frequency comb, using parametric frequency conversion394, overcoming passive cavity dispersion. The Kippenberg laboratory demonstrated with his group the accuracy of the mode spacing to be better than 1 part in 10(17) – hence unambiguously proving the comb nature5.

The discovery of microresonator frequency combs5,6 by the Kippenberg group in 2007 have made it possible to synthesize optical combs in compact devices that can be microfabricated on chip, with unprecedented high repetition rates in the technologically relevant gigahertz regime, and with optical bandwidths that are far beyond what can be achieved with conventional mode locked lasers. The original report, published in Nature in 2007, has opened a new field of research at the intersection of metrology and nano- and micro-photonics and nonlinear optics, which has led to numerous advances by dozens of highly recognized experimental and theoretical research groups and is an active frontier of research. Microresonator Kerr combs have been demonstrated now in a variety of platforms7–10 including the all important fully CMOS compatible platforms11,12. Their spectral coverage extended to the visible8 and mid infrared13,14, repetition rates in the microwave regimes have been achieved15. In addition, microresonator combs have been successfully applied to the field of coherent communication16, demonstrated for use in waveform synthesis17 and low noise microwave generation8 as well as the realization of compact atomic clocks18.
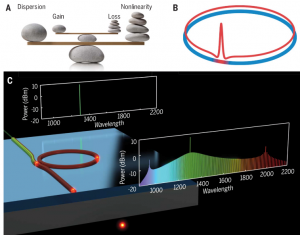
Kippenberg group also revealed their universal dynamics19, which culminated in the observation of low phase noise integrated silicon nitride frequency combs. In addition his research discovered for the first time dissipative cavity solitons in optical microresonators20; short bursts of optical pulses formed by the balance and interplay of nonlinearity and dispersion as well as parametric gain and loss. This has in particular in the last years led to major theoretical activities21,22 as it connected Kerr combs to dissipative temporal soliton Physics22, as described by the Lugiato Lefever equation23. Such soliton Kerr combs have in recent years proliferated and shown in a wide variety of platforms, ranging from crystalline resonators, chipscale silica disks to integrated devices. Using the soliton state enabled the EPFL team to demonstrate the counting of cycles of light using a microresonator24 . Moreover the EPFL research led to the first observation of soliton induced Cherenkov radiation25, enabling coherent and broadband combs. In joint work with KIT the EPFL team demonstrated the use of soliton microresonator comb for coherent communication26 at terabit per second, at both the receiver and transmitted side. The discovery of dissipative solitons in micro-resonators has enabled many other advances – as recently reviewed27 – notably dual comb spectroscopy28, counter-clockwise solitons29, dual soliton comb based distance measurements30,31, or synthesizing frequencies on chip32. Moreover, in addition to theoretically predicted dissipative soliton behavior such as breather soliton dynamics33–35, also new and theoretically not previously predicted dynamics has been observed ranging from formation of soliton crystals36, soliton switching37, and new type of breather solitons38. The soliton Kerr frequency combs thereby provided a highly fruitful new playground for fundamental nonlinear science and applications alike.
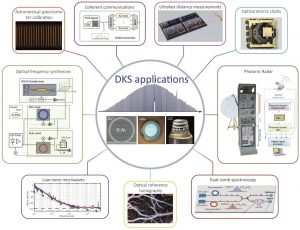
The disruptive potential of this discovery and the potential to advance technologies from metrology, sensing, timekeeping and spectroscopy has led to large funding initiatives in the US in recent years, such as DARPA SCOUT, DODOS and PULSE. It has become clear that optical combs are an area in which optical micro resonator research can actually lead to actual application outside the academic laboratory, but also can be equally useful in other areas of science. For instance, the large mode spacing achieved in these micro-combs (>10 GHz) makes these devices ideal for Astronomy to calibrate spectrometer39 in the quest to search explants39. The ability to create chipscale combs could contribute to making frequency metrology ubiquitous, and enable new applications that require large mode spacing.
Quotes from Literature:
“Such microcombs offer revolutionary advantages over existing comb technology, including chip-based photonic integration, uniquely large comb-mode spacings in the tens of gigahertz range, and monolithic construction with small size and power consumption. “18
Key publications on: Microresonator frequency combs
Del’Haye, P. et al. Optical frequency comb generation from a monolithic microresonator. Nature 450, 1214–1217 (2007).
Brasch, V. et al. Photonic chip–based optical frequency comb using soliton Cherenkov radiation. Science aad4811 (2015). doi:10.1126/science.aad4811
Herr, T. et al. Universal formation dynamics and noise of Kerr-frequency combs in microresonators. Nat. Photonics 6, 480–487 (2012).
Del’Haye, P. et al. Octave Spanning Tunable Frequency Comb from a Microresonator. Phys. Rev. Lett. 107, 063901 (2011).
Pfeifle, J. et al. Coherent terabit communications with microresonator Kerr frequency combs. Nat. Photonics 8, 375–380 (2014).
Herr, T. et al. Temporal solitons in optical microresonators. Nat. Photonics 8, 145–152 (2014).
Kippenberg, T. J., Holzwarth, R. & Diddams, S. A. Microresonator-Based Optical Frequency Combs. Science 332, 555–559 (2011).
Del’Haye, P., Arcizet, O., Gorodetsky, M. L., Holzwarth, R. & Kippenberg, T. J. Frequency comb assisted diode laser spectroscopy for measurement of microcavity dispersion. Nat. Photonics 3, 529–533 (2009).
Guo, H. et al. Universal dynamics and deterministic switching of dissipative Kerr solitons in optical microresonators. Nat. Phys. (2016).
Marin-Palomo, P. et al. Microresonator-based solitons for massively parallel coherent optical communications. Nature 546, 274–279 (2017).
Trocha et al. Ultrafast distance measurement with Microresonator-based frequency combs. Science (in press) (2018).
References
- Udem, T., Holzwarth, R. & Hänsch, T. W. Optical frequency metrology. Nature 416, 233–237 (2002).
- Diddams, S. A. et al. Direct link between microwave and optical frequencies with a 300 THz femtosecond laser comb. Physical Review Letters 84, 5102 (2000).
- Matsko, A. B., Savchenkov, A. A., Strekalov, D., Ilchenko, V. S. & Maleki, L. Optical hyperparametric oscillations in a whispering-gallery-mode resonator: Threshold and phase diffusion. Physical Review A 71, (2005).
- Kippenberg, T. J., Spillane, S. M. & Vahala, K. J. Kerr-Nonlinearity Optical Parametric Oscillation in an Ultrahigh- Q Toroid Microcavity. Physical Review Letters 93, (2004).
- Del’Haye, P. et al. Optical frequency comb generation from a monolithic microresonator. Nature 450, 1214–1217 (2007).
- Kippenberg, T. J., Holzwarth, R. & Diddams, S. A. Microresonator-Based Optical Frequency Combs. Science 332, 555–559 (2011).
- Papp, S. B., Del’Haye, P. & Diddams, S. A. Mechanical Control of a Microrod-Resonator Optical Frequency Comb. Phys. Rev. X 3, 031003 (2013).
- Savchenkov, A. A. et al. Kerr combs with selectable central frequency. Nature Photonics 5, 293–296 (2011).
- Levy, J. S. et al. CMOS-compatible multiple-wavelength oscillator for on-chip optical interconnects. Nature Photonics 4, 37–40 (2010).
- Hausmann, B. J. M., Bulu, I., Venkataraman, V., Deotare, P. & Lončar, M. Diamond nonlinear photonics. Nat Photon 8, 369–374 (2014).
- Foster, M. A. et al. Silicon-based monolithic optical frequency comb source. Optics Express 19, 14233–14239 (2011).
- Moss, D. J., Morandotti, R., Gaeta, A. L. & Lipson, M. New CMOS-compatible platforms based on silicon nitride and Hydex for nonlinear optics. Nature Photonics 7, 597–607 (2013).
- Wang, C. Y. et al. Mid-infrared optical frequency combs at 2.5 μm based on crystalline microresonators. Nature Communications 4, 1345 (2013).
- Griffith, A. G. et al. Silicon-chip mid-infrared frequency comb generation. Nature Communications 6, 6299 (2015).
- Yi, X., Yang, Q.-F., Yang, K. Y., Suh, M.-G. & Vahala, K. Soliton frequency comb at microwave rates in a high-Q silica microresonator. Optica 2, 1078 (2015).
- Pfeifle, J. et al. Coherent terabit communications with microresonator Kerr frequency combs. Nat Photon 8, 375–380 (2014).
- Ferdous, F. et al. Spectral line-by-line pulse shaping of on-chip microresonator frequency combs. Nature Photonics 5, 770–776 (2011).
- Papp, S. B. et al. Microresonator frequency comb optical clock. Optica 1, 10 (2014).
- Herr, T. et al. Universal formation dynamics and noise of Kerr-frequency combs in microresonators. Nat Photon 6, 480–487 (2012).
- Herr, T. et al. Temporal solitons in optical microresonators. Nat Photon 8, 145–152 (2014).
- Coen, S. & Erkintalo, M. Universal scaling laws of Kerr frequency combs. Optics letters 38, 1790–1792 (2013).
- Chembo, Y. K. & Menyuk, C. R. Spatiotemporal Lugiato-Lefever formalism for Kerr-comb generation in whispering-gallery-mode resonators. Physical Review A 87, (2013).
- Lugiato, L. A. & Lefever, R. Spatial Dissipative Structures in Passive Optical Systems. Phys. Rev. Lett. 58, 2209–2211 (1987).
- Jost, J. D. et al. Counting the cycles of light using a self-referenced optical microresonator. Optica 2, 706 (2015).
- Brasch, V. et al. Photonic chip–based optical frequency comb using soliton Cherenkov radiation. Science aad4811 (2015) doi:10.1126/science.aad4811.
- Marin-Palomo, P. et al. Microresonator-based solitons for massively parallel coherent optical communications. Nature 546, 274–279 (2017).
- Weiner, A. M. Frequency combs: Cavity solitons come of age. Nat Photon 11, 533–535 (2017).
- Suh, M.-G., Yang, Q.-F., Yang, K. Y., Yi, X. & Vahala, K. J. Microresonator soliton dual-comb spectroscopy. Science aah6516 (2016) doi:10.1126/science.aah6516.
- Yang, Q.-F., Yi, X., Yang, K. Y. & Vahala, K. Counter-propagating solitons in microresonators. Nature Photonics (2017) doi:10.1038/nphoton.2017.117.
- Suh, M.-G. & Vahala, K. Soliton Microcomb Range Measurement. arXiv:1705.06697 [physics] (2017).
- Trocha, P. et al. Ultrafast optical ranging using microresonator soliton frequency combs. arXiv:1707.05969 [physics] (2017).
- Spencer, D. T. et al. An Integrated-Photonics Optical-Frequency Synthesizer. arXiv:1708.05228 [physics] (2017).
- Bao, C. et al. Observation of Fermi-Pasta-Ulam Recurrence Induced by Breather Solitons in an Optical Microresonator. Physical Review Letters 117, (2016).
- Yu, M. et al. Breather soliton dynamics in microresonators. Nature Communications 8, 14569 (2017).
- Matsko, A. B., Savchenkov, A. A. & Maleki, L. On excitation of breather solitons in an optical microresonator. Optics letters 37, 4856–4858 (2012).
- Cole, D. C., Lamb, E. S., Del’Haye, P., Diddams, S. A. & Papp, S. B. Soliton crystals in Kerr resonators. arXiv:1610.00080 [physics] (2016).
- Guo, H. et al. Universal dynamics and deterministic switching of dissipative Kerr solitons in optical microresonators. Nat Phys advance online publication, (2016).
- Guo, H. et al. Inter-mode breather solitons in optical microresonators. arXiv:1705.05003 [physics] (2017).
- Wilken, T. et al. A spectrograph for exoplanet observations calibrated at the centimetre-per-second level. Nature 485, 611–614 (2012).